 |
Validation d'instruments de mesure |
Les relations client fournisseur se font souvent sous la forme d'acceptation ou de rejet d'un lot de pièces en fonction d'un taux de non conformes.
Ici on va procéder à la vérification d'un appareil de production ou de mesure.
Un bon appareil étant celui qui mesure ou fournit la précision demandée.
Ici alpha va désigner la probabilité d'accepter un mauvais appareil
Bêta va désigner la probabilité de refuser un bon appareil.
Ces deux probabilités ne sont pas complémentaires. Si on a 10% de chance d'accepter un mauvais appareil on a pas 90% de chances d'avoir un bon.
Pour pouvoir donc faire le bon distinguo on va choisir des limites pour un exemple avant de généraliser :
On va dire que l'appareil est de bonne qualité si sa précision est d'une graduation.
On devra le rejeter si sa précision est de deux graduations.
On sait que quand on fait un prélèvement la variable :
![]() suit une loi du khi 2 à n-1 ddl.
suit une loi du khi 2 à n-1 ddl.
La loi du khi 2 est une loi de probabilité de cette forme.
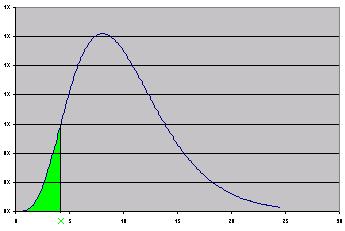
Mais on se sert surtout de la loi cumulée qui donne pour un point x choisi la surface verte qui correspond à la probabilité d'être inférieur à x.
Dans notre cas pour estimer une loi on prend comme valeur de l'écart type sigma la précision choisie. Pour un échantillon donné on aura deux variables une avec 1^2=1 au dénominateur et l'autre avec 2^2=4 au dénominateur : c'est comme si on avait deux lois différentes.
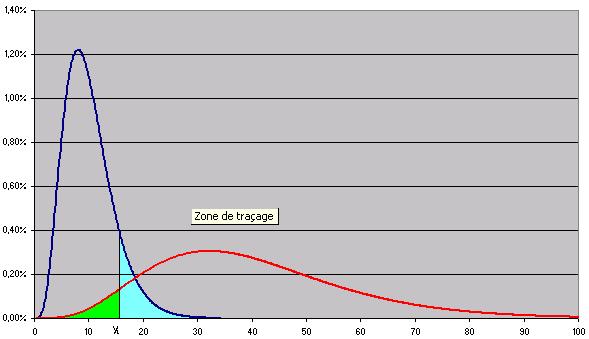
Ici on représente ces deux lois avec en bleu la loi sigma = 1 et en rouge la loi sigma = 2.
A chaque mesure on va donc pouvoir estimer les deux zones :
La zone bleue clair qui représente la probabilité de rejeter un bon appareil bêta
La zone verte qui représente la probabilité d'accepter un mauvais appareil alpha
Si on prend un graphique cumulé on a une lecture directe.
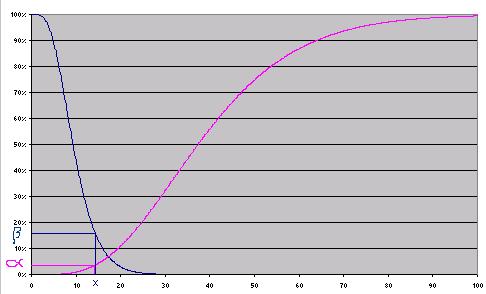
Donc pour une mesure donnée on estime une valeur de la variable de décision qui dépend de l'écart type.
Car le haut de la fraction = (n-1)*sigma^2
On constate sur le graphe que si on accepte des appareils dont sigma est fort, la probabilité de rejeter un bon appareil diminue. Mais dans le même temps la probabilité d'accepter un mauvais aussi.
Les deux courbes sont liées dès que l'on choisit un risque alpha par exemple le risque bêta correspondant vient immédiatement . on peut donc lier sigma, alpha, bêta, le nbr de ddl et donc d'expériences, et les précisions d'acceptation et de rejet.
Pour faire un choix en utilisant les statistiques il faut en premier définir une stratégie d'essai. il y a beaucoup de paramètres à prendre en compte.
En voici les principaux :
La probabilité d'accepter un mauvais appareil : alpha,
La probabilité de refuser un bon appareil : bêta,
La valeur maximale acceptable,
La valeur minimale rejetable,
Le nombre d'expériences.
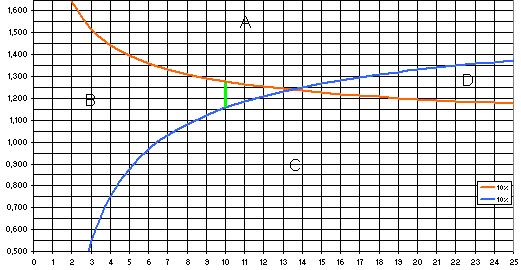
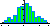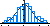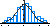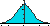
Le graphique représente les choix en fonction de % de refus ou d'acceptation
L'axe x correspond au nombre d'expériences effectuées
L'axe y reprend l'écart type mesuré.
Ici on choisit comme écart de mesure bon 1 graduation et comme écart inacceptable 1,7 graduations.
Les probabilités alpha et bêta sont prises toutes les deux égales à 10%.
La courbe montante sépare le plan suivant la probabilité alpha :
Au dessus il y a plus de 10% de chance d'accepter un mauvais appareil
La courbe descendante sépare le plan suivant la probabilité bêta :
En dessous il y a plus de 10% de chance de rejeter un bon appareil
Ces deux courbes séparent le plan en quatre zones
A zone de rejet de l'appareil
C zone d'acceptation de l'appareil
B zone de doute
D zone de précision supérieure
On voit que le nombre d'expériences a une influence sur la probabilité de tomber dans une zone de doute. Par exemple si on fait 10 mesures on s'aperçoit qu'on peut tomber dans la zone verte et l'on ne pourra alors pas statuer sur le sort de l'appareil.
remarque sur la zone D
dès que l'on choisit un nombre d'expériences supérieur à 13 on pourrait y faire se couper deux courbes de probabilités alpha et béta inférieures. C'est à dire que si les probabilités alpha et béta actuelles sont acceptées par les deux parties cela ne fait qu'augmenter le coût de la vérification.
L'idée la plus simple en voyant ce graphique est de faire 13 mesures puisque ça correspond à l'intersection des deux courbes et que donc il suffit de calculer l'écart type : si il est supérieur à 1.25 on rejette l'appareil sinon on l'accepte.
Une connaissance plus approfondie des appareils peut nous permettre de diminuer le nombre de mesures le protocole devient donc pour 10 expériences :
Calculer l'écart type
Si il est inférieur à 1,15 accepter l'appareil
Si il est supérieur à 1,26 rejeter l'appareil
Si il est entre 1,15 et 1,26 faire 13 mesures et décider comme précédemment
Le choix d'un protocole plutôt qu'un autre dépend surtout de la connaissance que l'on a des appareils en général. Par exemple si l'écart type est en général très faible on va choisir de ne faire que 7 ou 8 expériences. Puis en cas de doute on va alors en faire 13.
Par contre si il y a souvent doute on va faire systématiquement 13 expériences.