LES RESULTATS

Présentation des résultats avec comparaison avec les méthodes statistiques.

Soit le processus de décision suivant : on considère que l’on a affaire à

un doublon si la sortie est supérieure à 0,5
un non doublon si la sortie est inférieure à -0,5
un indéterminé si la sortie est entre -0,5 et 0,5

Le taux d’indéterminés est au tour de 5 %
on peut voir cette répartition sur le graphique suivant :

l'axe x représente la valeur de l'expert
l'axe y donne la réponse du réseau
en haut à droite : les doublons bien classés
en bas à droite : les doublons mal classés
en bas à gauche : les non doublons bien classés
en haut à gauche : les non doublons mal classés
entre les deux horizontales -0,5 et 0,5 les indéterminés

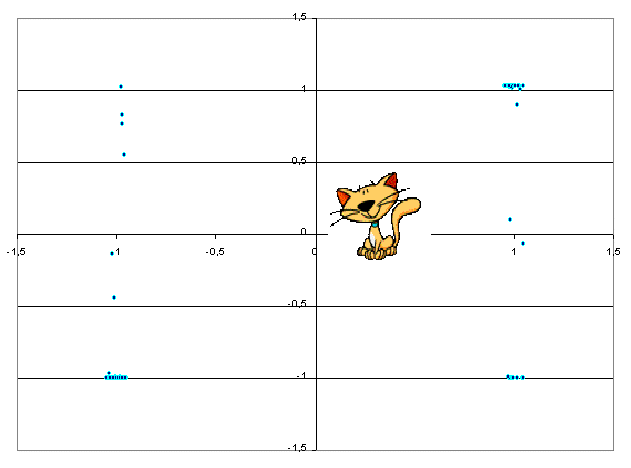
Le graphique suivant montre le pouvoir discriminant du réseau puisque très peu de réponses sont indéterminées : entre les deux pics (gauche non doublons, droite doublons).

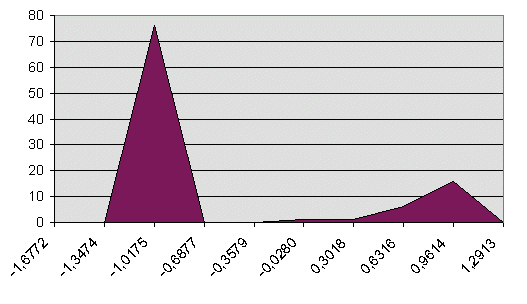
Sachant que dans notre base de validation le taux de doublons est de moins de 9% et en considérant les indéterminés comme n’étant pas des erreurs on a :

taux d’erreur sur les doublons : 9,6%
taux d’erreur sur les non doublons : 3,8%
taux d’erreur global sur la base : 4,6%

Ces résultats sont à comparer avec ceux d’une analyse discriminante où les paramètres sont calculés sur la base d’apprentissage.
Dans ce cas là j’ai pris les résultats bruts totaux ce qui donne sur la base de validation un taux d’erreur de 8.64%
On les compare donc au taux d’erreur total du réseau de neurones en comptant comme erreurs les indéterminés. Dans ce cas les résultats du réseau de neurones sont de 7.70% d’erreurs.
L’avantage est donc de près de 1% pour le réseau de neurones.

CONCLUSION

Cet exemple permet de voir plusieurs choses :
Un projet tel que celui ci prend un certain temps en particulier dans la création et la mise en forme de la base d'exemples.

Il est possible et raisonnablement faisable de calculer les poids d’un réseau modeste en utilisant un tableur. Ceci est d’autant plus vrai que les ordinateurs personnels sont de plus en plus rapides et les outils bureautiques intuitifs, souples et puissants.

Ceci donne un taux de réussite de plus de 95% ce qui permet de penser que l’outil présenté bénéficie de l'utilisation du réseau de neurones. Par contre dès qu'il y a une couche cachée, l'interprétation des poids pour trouver une règle utilisable devient presque impossible.

Contactez-moi pour tout projet, question ou commentaire.