| |
Graduations d'un instrument de mesure
|
Le vernier est un dispositif permettant de lire une mesure sur des appareils comme le pied à coulisse ou un micromètre.
Sans cet outil ces mesures seraient illisibles : imaginez une règle graduée au dixième de millimètre.
Soit un segment de longueur 1 unité fractionné en n divisions.
Une partie mobile de longueur une unité moins une division.
Cette partie mobile est fractionnée en n divisions.
La précision est de 1/n2
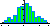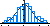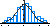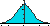
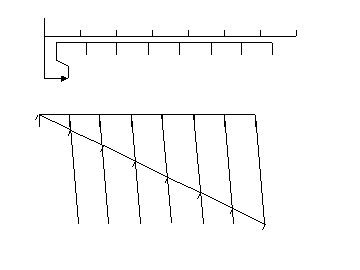Le graphique du haut représente les deux parties du vernier. La flèche elle matérialise la grandeur à mesurer.
Le graphique du dessous rappelle comment on obtient la division en n parties égales un segment :
On prend un segment de longueur indéfinie mais séparée en n parties égales (au compas) et ayant la même origine que l'autre segment.
On trace la droite joignant les deux extrémités des segments. Puis les parallèles à cette droite passant par les différentes séparations. Ces droites coupent le premier segment de manière à le séparer comme prévu (de par le théorème de Thalès).
Soit un déplacement de la partie mobile de k/n2 unité (k<n)
calculons la distance entre l'origine et la graduation k du vernier.
d=k/n2.k(n-1)/n2=k/n2+k/n-k/n2=k/n.
On vérifie donc que la graduation k du vernier se trouve en face de la graduation k de la règle ce qui montre comment interpréter la lecture et démontre la précision de l'appareil.
Ici les segments sont fractionnés en 7 divisions.
La précision va donc être de 1/(7*7)=1/49
Les deuxièmes graduations étant en face la valeur mesurée = 2/49*la longueur du grand segment. Soit environ 4% de la longueur du grand segment ce que vous pouvez vérifier avec une règle.
distance entre l'origine et une graduation k du vernier.
d=k/n2+jg(n-1)/n2 ---> posons g=k+e
d=k/n2+(k+e)(n-1)/n2=k/n2+(k+e)/n-k/n2-e/n2=k/n+e/n-e/n2
on retombe en face d'une graduation que si
e=o*n--->d=k/n+(o*n)/n-(o*n)/n2=k/n-o/n+o
le terme o veut dire que l'on a dépassé la première graduation
La précision statistique d'un appareil de mesure dépend de sa conception.
Imaginez une règle faite dans un matériau élastique et vous lirez des mesures aléatoires.
Mais à l'inverse une règle en platine graduée uniquement tous les centimètres n'est pas d'une très grande utilité. On évalue donc l'écart de mesure dû à la graduation.
Pied à coulisse en ivoire.
Pour vous entraîner j'ai conçu un classeur Excel permettant de simuler un vernier de pied à coulisse. Son fonctionnement est simple : à l'aide du curseur horizontal vous déplacez la partie mobile. Vous effectuez la mesure puis comparez avec le résultat que l'on affiche en cochant une case.
Ce classeur simple et sans macro est disponible en téléchargement en utilisant le système de micropaiement suivant.
Pour indication, le tarif pour la France est de 1,68 euros. Pour ceux se connectant par modem le mot de passe peut être obtenu en dehors de la connection ou en utilisant votre portable.
Bonus : en plus le classeur contient aussi un entrainement à la lecture d'un micromètre
|
|
Le micromètre ou palmer est un instrument de précision qu’on doit utiliser avec soin. Il est muni d’un tambour qui tourne autour d’une règle graduée. Le micromètre est choisi en fonction de la pièce à mesurer (0 à 25mm, 25 à 50mm, …). La précision est de 0,01 à 0,001mm. Il doit être étalonné à l’aide d’une cale de référence.
On doit insérer l’objet à mesurer dans les mâchoires du micromètre. L’approche se fait à l’aide du tambour gradué, le serrage de la pièce se fait à l’aide de la molette limiteur d’effort.
La règle fixe est graduée au demimillimètre. Un tour du tambour correspond à 0,5 mm et 50 graduations du tambour
Les graduations valent 0,01 mm.
exemple 1 : La règle fixe indique 21 mm et le tambour indique 0,26 mm.
Donc la mesure est : 21 mm + 0, 26 mm = 21, 26 mm
exemple 2 : la règle fixe indique 22,5 mm et le tambour indique 0,06 mm.
La mesure est alors : 22,5 mm+ 0,06 mm= 22,56 mm
Le classeur excel pour s'entraîner à la lecture d'un vernier contient aussi l'entraînement à la lecture d'un micromètre.
|
|
 |
 |
