 |
Calculs des erreurs dues à l'arrondi de l'affichage |
L'erreur que l'on va calculer maintenant est présente deux fois
La première fois quand on règle la machine à 0. En effet on la règle à zéro en se fiant à l'affichage.
La seconde fois c'est à chaque mesure.
La variance totale due à l'affichage est le double de l'erreur d'arrondi :
![]()
![]()
Pour une unité d'affichage donnée on arrondit au dessus pour 0,5 ou plus. Et on arrondit au dessous pour les décimales inférieures à 0,5.
Calcul de l'erreur d'arrondi quand l'afficheur est numérique. On calcule l'erreur sur la partie de 0 à la moitié de la graduation. R est la taille de la graduation et à partir de 0.5 on passe à la graduation suivante.
Si la graduation est de 10g : on a entre 0 et 5 grammes :
Pour 1 g l'affichage est de 0g soit 1 d'erreur 1^2 pour l'erreur quadratique
Pour 2 g l'affichage est de 0g soit 2 d'erreur 2^2 pour l'erreur quadratique
Pour x g l'affichage est de 0g soit x d'erreur x^2 pour l'erreur quadratique
Soit une erreur quadratique totale de
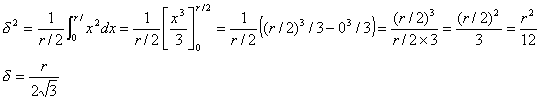
(r est la taille de la graduation)
le calcul entre 0 et 0,5 suffit car entre 0,5 et 1 c'est une courbe symétrique
L'erreur totale de l'affichage est donc de (les variances sont ajoutées) :
![]()
cas1
Si l'afficheur n'arrondit pas à partir de 0.5 l'erreur continue à augmenter entre 0.5r et r soit:
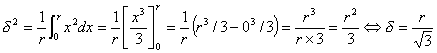
L'erreur totale en considérant l'erreur lors du réglage du zéro est donc :
![]()
cas2
Dans le cas de l'afficheur analogique on considère que l'erreur est une loi normale où l'on a toutes les valeurs entre les deux graduations. Dans une loi normale on a 99.99% des valeurs entre m+/- 3écarts-type.
Donc sigma = r/6
L'erreur totale en considérant l'erreur lors du réglage du zéro est donc :
![]()
Voir aussi :