Chaque neurone prend comme entrées ei toutes les sorties de la couche précédente. Chaque entrée ei est multipliée par un poids correspondant wi. Le seuil w0 est une constante. Le sommateur calcule l’entrée du neurone A. La fonction d’activation f calcule la sortie.
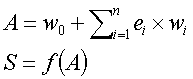
La fonction d’activation choisie est une sygmoïde.
Notre réseau prend en entrée les 9 notes qui sont prises en compte par une couche d'entrée de 5 neurones. Une couche cachée de trois neurones est entièrement connectée aux neurones d'entrée et fournit ses données à un unique neurone de sortie. La valeur proposée par le réseau est comparée à la valeur trouvée manuellement. L'écart permet par rétropropagation de mettre à jour tous les poids.
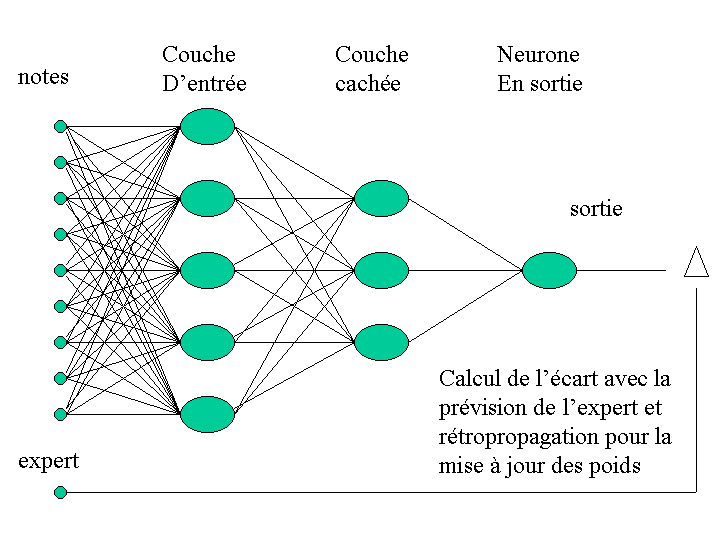
On retrouve ce shéma dans la construction dans Excel
A gauche les paramètres d'entrée avec en dessous la prévision de l'expert.
entre l'entrée et le neurone de sortie les 5 neurones de la couche d'entrée et les trois de la couche intermédiaire. Cette partie du classeur montre les calculs des sorties et la rétropopagation des écarts (zi) mais ne comprend pas le calcul des poids (wi) pour l'étape suivante.
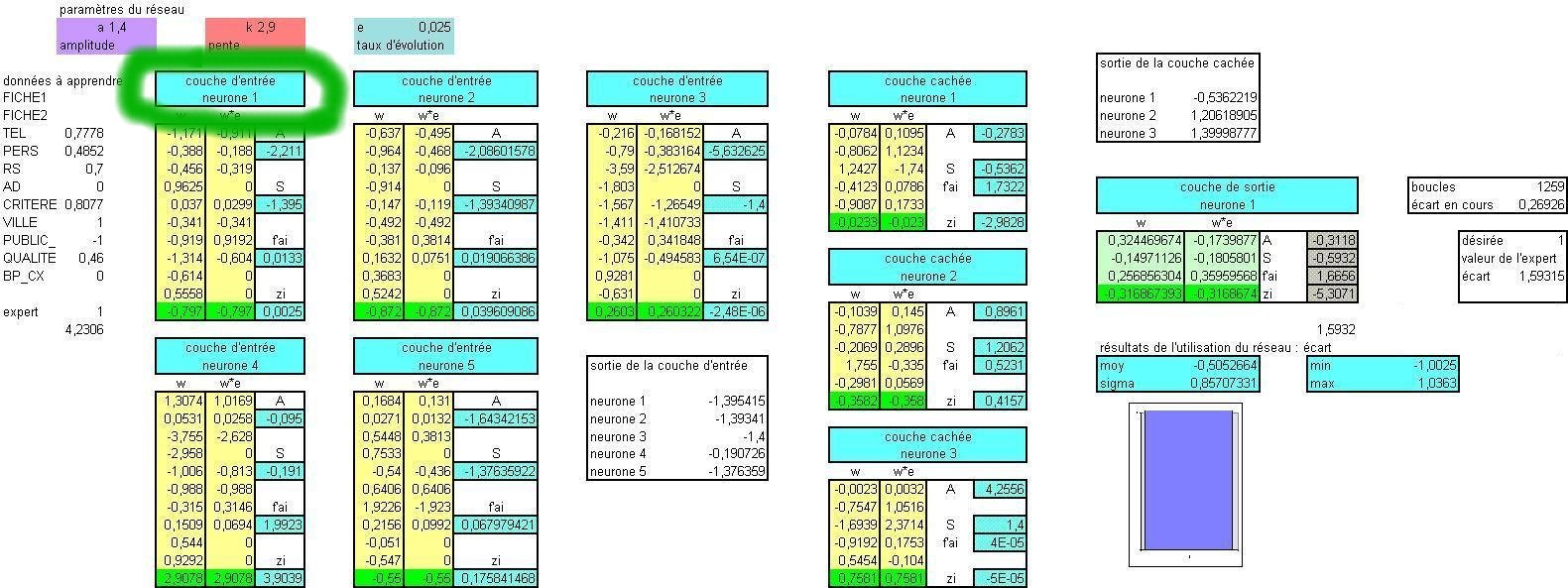
Tous les poids (w) affichés dans chaque neurone ne sont pas des valeurs mais des formules.
Ces formules font référence à un tableau où se trouvent les valeurs des poids et où ils sont modifiés d'étape en étape.
A chaque présentation d’un exemple on recalcule les poids en tenant compte de la justesse ou non de la prévision du réseau. Pour un poids w recevant e comme entrée la nouvelle valeur de w est :
![]()
epsilon (pas du gradient) est un taux d’évolution que je fais décroître en fonction de l’apprentissage. Ce paramètre est saisi en haut sur la feuille précédente (e pas du gradient).
Le principe de l’apprentissage dans Excel est simple. On place dans un cadre les paramètres de l’étape h. Dans un cadre de même format se calculent les paramètres pour l’étape h+1.
Je sélectionne ces résultat et je les colle à la place des anciennes valeurs.
Il suffit donc d’utiliser la macro suivante qui boucle 200 fois
Macro1
=POUR("I";1;L(4)C;1)
=COLLAGE.SPECIAL(3;1;FAUX;FAUX)
=SUIVANT()
=RETOUR()
200
Les paramètres calculés en plus des poids sont :
Le numéro de la ligne où se trouve l’exemple c'est le chiffre en dessous des poids du neurone de sortie. En général on choisit la ligne suivante (on augmente de 1).
L’erreur sur la base d’apprentissage :
Pour simplifier et rester dans le même cadre que le copier coller vu plus haut j’utilise une moyenne mobile géométrique : chiffre en haut à droite au dessus du neurone de sortie.
![]()
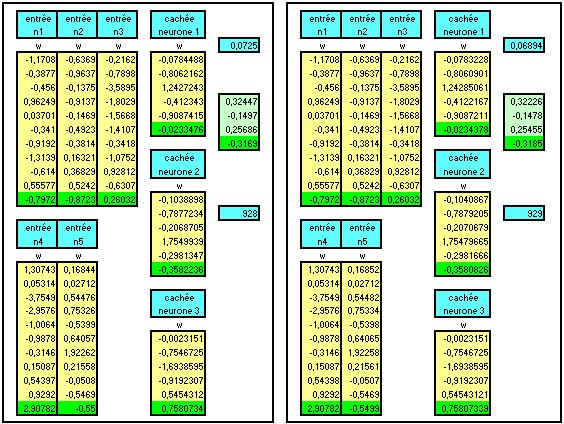
Les poids sont initialisés de manière aléatoire. Epsilon est entre 0.1 et 0.5
On fait plusieurs boucles jusqu’à ce que l’erreur E devienne raisonnable.
Je diminue epsilon .
On recommence mais avec plus de précautions.
Dès que E diminue on fait une sauvegarde des paramètres du réseau.
Périodiquement on fait une sauvegarde de niveau 2. C’est une sauvegarde de la sauvegarde pour pouvoir se récupérer si le réseau se met à diverger. Dans le cas où le réseau diverge on reprend la sauvegarde de niveau 2 et on repart après avoir diminué epsilon.
On en profite pour faire un test sur la base de validation.
Quand le réseau ne converge plus on diminue le taux d’évolution epsilon jusqu’à ce qu’il n’y ait plus de progrès.
La procédure est recommencée plusieurs fois et on garde la meilleure solution.
Pour ceux qui veulent voir de plus près un classeur exemple à télécharger gratuitement 91ko.