Bases de probabilités
Les lois de probabilités
Régression linéaire

Bases de probabilités |
Analyse en composantes principales (ACP) |
Problème :
La plupart des résultats d'enquêtes ou de mesures se présentent sous forme de tableaux de données avec en ligne les individus mesurés, et en colonnes chacune des valeurs mesurées. On se place ici dans le cas où les mesures sont des nombres (valeurs quantitatives). Si on a 20 questions * 100 individus cela fait un nuage de points en 20 dimensions. Comme on a l'habitude de travailler dans un espace à 3 dimensions on peut voir un objet, mais pour faire un rapport et interpréter ces données on utilise des graphiques. C'est à dire un document en 2 dimensions. Une première solution consisterait à prendre chacune des colonnes 2 à 2 pour faire tous les graphes de toutes les combinaisons de variables. Cela donnerait environ 200 graphes, ce qui n'aide pas à synthétiser l'information. L'ACP a pour but de remplacer les 20 questions par quelques axes qui seront à la fois interprétables facilement et représentatifs de l'information contenue dans le nuage de points. C'est un peu comme faire une photo d'un objet : on passe de 3 à 2 dimensions. Le but de l'ACP est de trouver l'endroit où poser l'appareil photo pour que l'on reconnaisse le mieux le sujet.
Au départ le tableau contient des informations comme l'année, la température, le pourcentage de votants, une note... Toutes ces informations ont des unités différentes et en gardant celles-ci, une valeur comme l'année va écraser les autres colonnes et ainsi masquer leur importance.
Pour parer à ce problème on fait un centrage de chaque colonne : on soustrait la valeur de la moyenne de la colonne à chaque valeur. La nouvelle moyenne de la colonne va être 0.
Puis on fait une réduction de la colonne : c'est à dire que l'on va diviser chaque valeur par l'écart type de sa colonne. Le nouvel écart type de la colonne va être 1.
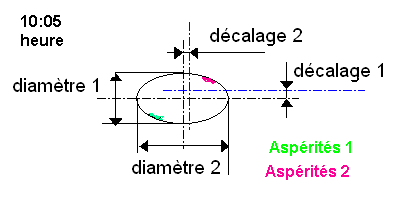
Mes connaissances du calcul matriciel étant anciennes et faibles je vais simplement indiquer les calculs que je fais dans mon classeur excel en utilisant un exemple. Suivi de production perçage de trous et mesure en ligne. Les grandeurs mesurées sont lues sur une image prise par une caméra numérique on mesure le diamètre sous 2 angles différents ainsi que le centrage par rapport à une position idéale. Une information concerne les copeaux qui peuvent rester. L'heure de la prise de vue est aussi notée.
Si on appelle D la matrice des données centrées réduites fabriquée au paragraphe précédent. t(D) est la matrice transposée de D (c'est à dire le tableau obtenu en mettant les individus comme colonne et les variables en lignes). J'ai calculé une matrice de variance covariance en 2 étapes
On obtient une matrice carrée avec en colonne et en ligne les noms des variables.
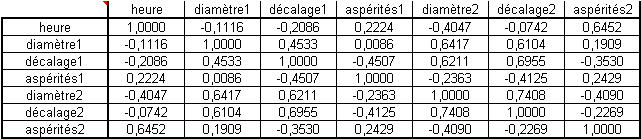
C'est de cette matrice que l'on va trouver les axes factoriels
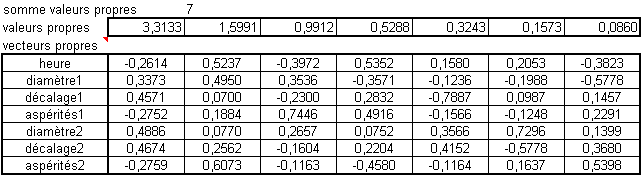
Pour cela on calcule les valeurs propres et les vecteurs propres associés. Les valeurs propres trouvées représentent la quantité d'information récupérée dans l'axe.
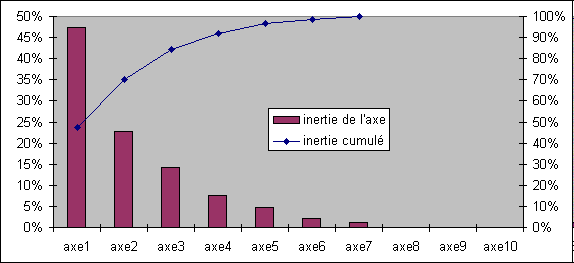
En divisant par le total des valeurs propres (qui est égal au nombre de variables si les données sont centrées réduites), on obtient cette valeur sous forme de pourcentage. La quantité d'information doit décroître rapidement sinon, cela veut dire que le nuage de points est de forme semblable à une sphère et que donc il n'y a aucun angle de prise de vue qui permette d'avoir une image satisfaisante.Ici on a 80% en cumulé dès le troisième axe.
Une fois ces axes calculés il faut en connaître la signification. pour cela on va regarder les projections des variables sur des plans formés par un couple d'axes factoriels. Les vecteurs propres sont multipliés par les racines des valeurs propres pour être affichés dans un cercle de rayon 1. On va regarder pour chaque axe factoriel quelles sont les variables qui se suivent et s'opposent. Au plus une variable a d'importance au plus elle sera représentée proche du cercle. Dans le cas contraire, une variable n'expliquant pas un axe se trouve vers le centre.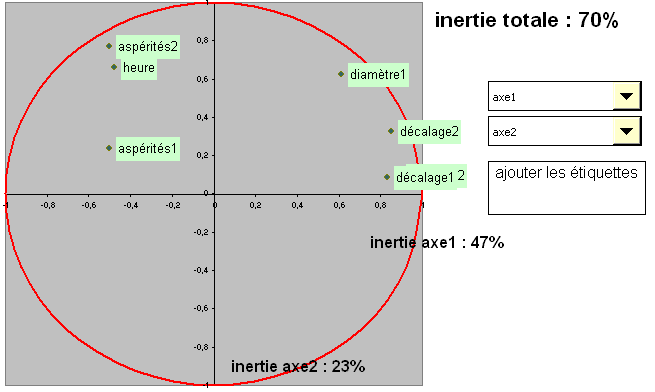
l'axe 1 correspond à la taille globale des diamètres. Le fait que les décalages se trouvent du côté des diamètres tend à démontrer que ces deux valeurs sont liées.
L'axe vertical lui suit les aspérités 2, le diamètre 1 et les heures. Cela veut peut-être dire que les copaux s'accumulent avec le temps.
La variable aspérités 1 n'est pas représentées dans ce plan là (proche du centre), en fait si on regarde le tableau des vecteurs porpres on s'apperçoit que cette variable est confondue avec l'axe 3. Le menu déroulant permet de choisir la paire d'axes à afficher et cela se confirme sur la visualisation (non reproduite ici pour éviter de prendre trop de place).
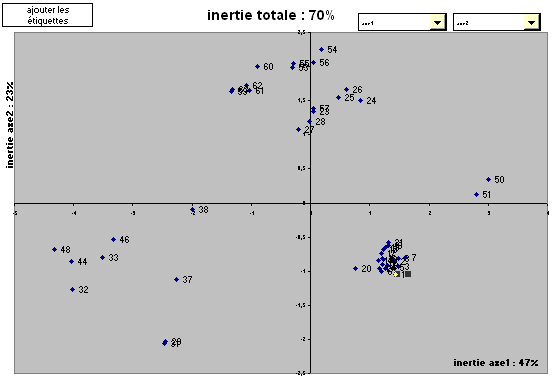
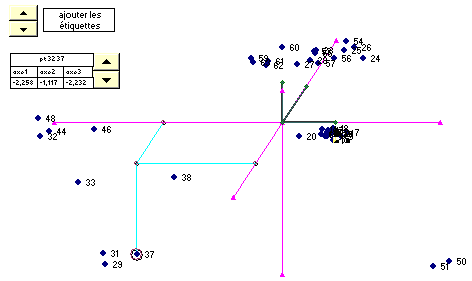
Voici une représentation des données sur les 3 premiers axes.
Alors que rien ne le laissait deviner, la population se sépare très nettement en trois groupes plus les valeurs 50 et 51. De plus on remarque que les heures ne se suivant pas (voir les indices des individus), on va pouvoir étudier le groupe d'en haut pour en déduire les causes de la présence d'aspérités. De même pour les valeurs de gauche qui doivent indiquer des conditions spéciales. On remarque que, en ce qui concerne le groupe des valeurs des pièces bonnes, il est très sérré, ce qui indique que sans la présence des causes qui créent les problèmes, la variabilité de la machine est très faible.
Pour trouver ces groupes de manière calculée, il existe des méthodes comme la classification ascendante hiérarchique qui agglutine de proche en proche tous les individus. Et la classification par nuées dynamiques qui rend plus homogènes des groupes déjà constitués. En général on commence par une analyse en composantes principales. On prend les projections sur les axes principaux comme nouvelles variables. Puis on lance une classification ascendante hiérarchique pour visualiser l'arbre hiérarchique. On regarde sur l'arbre le premier saut significatif pour en déduire le nombre de classes à retenir. Enfin à partir du regrouppement fait dans ces classes par la CAHI on lance une optimisation par les nuées dynamiques. Alors on obtient une segmentation à laquelle on peut donner du sens.
Exemple d'arbre que l'on pourrait obtenir :
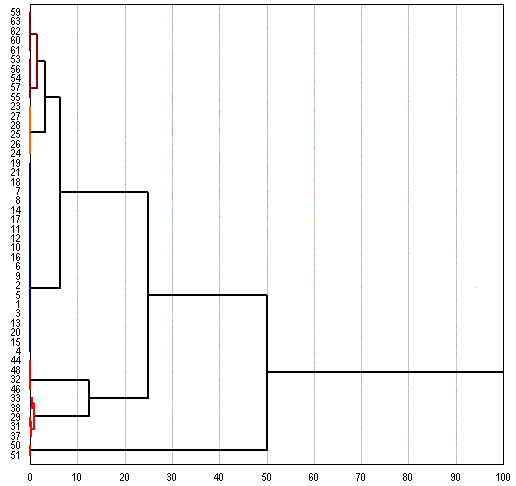
Le document ne fait pas de CAHI, mais il permet une classification de type kmean sur les 3 premiers axes factoriels avec un nombre de groupes de 2 à 7.