Bases de probabilités Vérification de la normalité régression linéaire

Domaine d'emploi des lois Hypergéométriques, de Bernoulli, des grands nombres et de Poisson

introduction

On tire n boules dans un sac qui en contient N dont D noires.
La loi de probabilité décrivant le nombre d de boules noires dans les n tirées est la loi hypergéométrique :

utilisation d'excel
p(d)=LOI.HYPERGEOMETRIQUE (d,n,D,N)

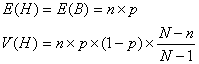
pour n<N/10 la loi hypergéométrique peut être approchée par une loi de Bernoulli avec :
p=D/N et k=d

Loi de Bernoulli ou binomiale
à utiliser dans le cas d'épreuves répétées : pile ou face ou tirage avec remise dans le sac.

V(B)=n*p*(1-p)

utilisation d'excel
p(d)=LOI.BINOMIALE (d,n,p,faux)
p(0)+p(1)+..+p(d)=LOI.BINOMIALE(d,n,p,vrai) probabilité d'avoir au plus d succès

• pour p<0,1 la loi de Bernoulli peut être approchée par une loi de Poisson avec v=np, k=d
• si alors la loi de Bernoulli peut être approchée par une loi normale avec x=k et v=np

loi de Poisson
E=V=v

utilisation d'excel
p(k)=LOI.POISSON(k;v;faux)
p(0)+p(1)+..+p(k)=LOI.POISSON(k,v,vrai)

pour v>25 la loi de Poisson est approchée par une loi normale avec x=k, E=V=v

Loi des grands nombres (normale / Laplace Gauss)

pour la variable

est normale réduite.

utilisation d'excel
p(z<=t)=LOI.NORMALE.STANDARD(t)

Ou bien on a la transformation suivante si f est la fréquence :

arcsin(racine(f)) suit une loi normale de moyenne arcsin(racine(p)) et d'écart-type racine (1/4n)