les cartes de contrôle
Les cartes de contrôle
- introduction
- calculs des limites dans un processus de moyenne et variance connue.
- initialisation des cartes pour un processus dont les paramètres sont estimés.
- efficacité d'une carte de contrôle
- cartes MA, (I, MR), EWMA
Tables et classeurs à télécharger
Calcul des limites de contrôle pour un processus suivant une loi normale de paramètres connus.
Procédé : X ~ N (μ0, σ0) à μ0, σ0 connus
m échantillons de taille n
le ième échantillon à X_i, si, R
Formules générales
méthode de Shewart : Limites de Contrôle à E(T)+- 3 σ(T) quelles que soit la loi de distribution de T.
méthode AFNOR : LC calculées telles que α= 0,2%
Carte moyenne X_
Méthode Shewhart
- points à tracer à x_i
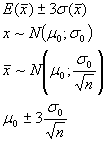
- ligne centraleà μ0
- limite supérieure de contrôle LSC à μ0 +(3/ √n)σ0
- limite inférieure de contrôle LIC à μ0 –(3/ √n )σ0
méthode Afnor UE 0,2%
- 0,2% à+-0,1%
- Si x suit une loi normale centrée réduite proba x>3,09=0,001 on remplace donc 3 par 3,09 dans le cas d’une loi normale.
La médiane
Attention, pour cette carte les données numériques ne sont pas extraites de tables mais d'une simulation faite dans excel. Si quelqu'un connait les vraies valeur, merci de me les faire parvenir.
La médiane est la donnée qui partage l'échantillon trié de telle sorte qu'il y en ait autant au dessus et en dessous.
Pour un échantillon de taille 3 trié la médiane est la deuxième valeur.
Pour un échantillon pair on prend la moyenne des 2 valeurs centrales (pour un échantillon de taille 6 on calcule la moyenne de la troisième et de la quatrième valeur).
Intérêts de la médiane
- elle ne nécessite aucun calcul dans un échantillon impair.
- elle est plus robuste que la carte moyenne, car insensible aux valeurs aberrantes.
On l'utilise surtout au début, quand le procédé n'est pas très bien maîtrisé.
paramètres de la carte de contrôle :
pour une loi normale (mais c'est aussi vrai pour toute loi symétrique)
ligne centrale : la moyenne
limites de contrôle 3 fois sigma médiane
La simulation sous excel pour une loi normale donne sigma médiane = sigma processus * coef
table des coefs trouvés en fonction de la taille de l'échantillon:
- n=3 --> 0,6655
- n=5 --> 0,5348
- n=7 --> 0,4592
- n=9 --> 0,4066
- n=11 --> 0,3664
Exemple
pour une variable suivant une loi normale de moyenne 14 et d'écart type 2
Carte médiane pour un échantillon de 5 pièces :
ligne centrale de la carte médiane :14
LSC = 14 + 3 *2*0,5348=17,21
LIC = 14 - 3 *2*0,5348= 10,7912
Carte S
Méthode de Shewhart E(s)+- 3 σ(s)
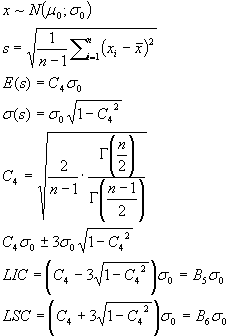
- Points à tracer si
- Ligne centrale C4*σ0
- LSC = B6 *σ0
- LIC = B5 *σ0
B5,B6,C4 tabulés
Carte S méthode Afnor (seules les limites changent)
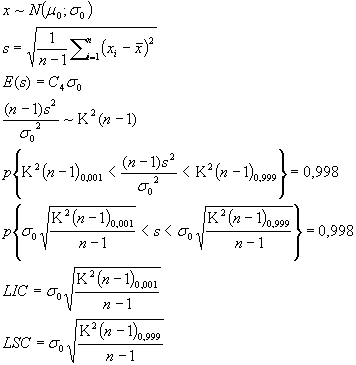
Carte étendues R
Méthode de shewhart
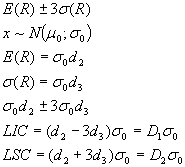
d2, d3 et D1, D2 tabulés
points à tracer Ri
ligne centrale d2 σ0
Méthode Afnor limites carte R
- points à tracer Ri
- ligne centrale d2 σ0
W étendue relative
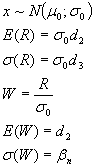
W0,001, W0,999 table de W
LSC=W0,999 σ0
LIC=W0,001 σ0
Classeur excel pour une carte moyenne étendue.
Travail quand les paramètres ne sont pas encore connus