Les plans d'expériences et la méthode Taguchi

Les statistiques de la qualité :

Plan de contrôle de réception.

Etude de capabilité d'un procédé

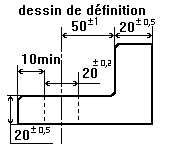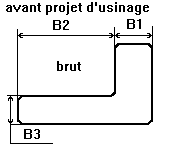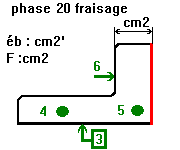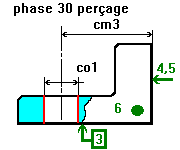
Les cartes de contrôle pour le suivi d'un processus dans le temps.

---

Une simulation d'usinage pour relier dessin de définition et les statistiques de la qualité.

Un nouvel ordonnancement utilisant la méthode OPT les PQR arbres et les algorithmes génétiques

Le wap : transmètre des informations sur le terrain

---

Recherche opérationnelle
Algorithme hongrois (Konig Egervary). Affectation de personnes à des tâches avec minimisation du coût total.

---

Les files d'attente

---

Mes coordonnées mes dernières réalisations et mon CV au format pdf

Un commentaire, un projet, une question : vos coordonnées : civilité madame mademoiselle monsieur prénom nom fonction société adresse CP ville tél fax mail de personnes pouvant être interressées par ce site : si vous avez créé un lien vers ce site sur quel site :

Les plans d'expériences s'inscrivent dans la démarche qualité au même titre que les autres outils statistiques : indices de capabilité, cartes de contrôle.
les indices de capabilité déterminent la possibilité qu'a l'outil de production de créer des pièces de bonne qualité.
Le SPC fourni aussi le concept de suivi statistique. Les cartes de contrôle vérifient dans le temps que les paramètres ayant servi au calcul des indices de capabilité restent d'actualité.
Enfin les plans d'expériences cherchent les causes d'une non qualité, ou plus positivement les paramètres pouvant améliorer la qualité actuelle.

Avantages des plans d'expériences

Les plans permettent une diminution considérable du nombre d'essais et une interprétation rapide et sans équivoque. Ils fournissent des résultats faciles à présenter à des non spécialistes.

Possibilité d'étudier un très grand nombre de facteurs
détection des interactions éventuelles
modélisation aisée des résultats
détermination des résultats avec une bonne précision.

Avantages des plans d'expériences sur un exemple

2 stratégies d'expérimentation : étude d'un pistolet à peinture
les deux facteurs influents mesurés : ouverture et pression

facteurs	mini	maxi
A ouverture	1 cran	3 crans
B pression	1 bar	2 bars

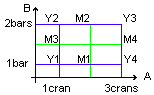
stratégie 1 Mi : on positionne un facteur sur la moyenne et on fait varier l'autre
effet de B mesuré grâce à M1 et M2
effet de A mesuré grâce à M3 et M4

stratégie 2 Yi : plan d'expériences
effet de A mesuré à l'aide de Y1, Y2, Y3, Y4
effet de B mesuré à l'aide de Y1, Y2, Y3, Y4

la stratégie 2 est bien meilleure que la 1 car les effets de chacun des facteurs sont mesurés à l'aide de 4 expérience.
Ceci donne une meilleure précision des résultats car la dispersion est inférieure.
De plus on peut étudier les interactions ce qui est impossible avec la première stratégie.

Les stratégies d'expérimentation

Calcul des effets
calculer la moyenne générale M
effet du facteur A au niveau 1
EA1=(moyenne des réponses avec A=1) - M
la somme des effets de A à tous ses niveaux est égale à 0
si A a trois niveaux il suffit d'en connaître 2 pour avoir le troisième.

Les plans d'expériences fractionnaires

la condition d'orthogonalité permet d'étudier l'effet d'un facteur indépendamment des autres facteurs à partir des résultats du plan.
ex système 2 facteurs à 2 niveaux : lorsque A est calculé il faut que B soit autant de fois au niveau 1 qu'au niveau 2 sinon son effet biaiserait celui de A

CNS d'orthogonalité de deux actions : à chaque niveau de l'une tous les niveaux de l'autre sont associé le même nombre de fois dans le plan d'expériences

orthogonalité d'un plan d'expériences :
un plan d'expériences est orthogonal vis à vis d'un modèle si toutes les actions disjointes du modèle sont orthogonales dans le plan

vérification de l'orthogonalité tableau d'incidence

CN non (suffisante) : un plan doit être le PPCM du produit du nombre de niveaux de toutes ses actions prises deux à deux.

exemple : Y=I+A+B+C+D+BC+CD
ABD 3 niveaux
C deux niveaux
BC et CD 2*3=6niveaux
* interactions non disjointes

A	3	*
B	3	3^2	*
C	2	2x3	2x3	*
D	3	3^2	3^2	2x3	*
BC	2x3	2x3^2	*	*	2x3^2	*
CD	2x3	2x3^2	2x3^2	*	*	*	*
		3	3	2	3	2x3	2x3
		A	B	C	D	BC	CD

PPCM = produit de tous les nombres premiers du tableau intervenant à leur puissance la plus élevée : 2*3^2=18

Condition sur le nombre de ddl

Le nombre minimal d'expériences à réaliser est égal au nombre de ddl du système étudié.
Pour étudier le modèle complet (avec toutes les interactions) il est nécessaire d'étudier le plan factoriel.

Résumé
la règle de l'orthogonalité dit que le nombre de lignes du plan doit être multiple de k (18)
la règle des ddl dit que le nombre de lignes doit être supérieur à

Y~	I	A	B	C	D	BC	CD
niveaux		3	3	2	3	2*3	2*3
ddl	1	2	2	1	2	1*2	1*2	=	12

Supérieur à 12 et multiple de 18 donc 18 essais

recherche de plans minimum

• avoir des nombres de niveaux premiers entre eux augmente considérablement le nombre d'essais
• étudier des interactions disjointes (AB et CD) augmente considérablement le nombre d'essais

notion d'alias plans 2^n (2 niveaux)

colonnes d'interactions 1*1=2, 2*2=2, 1*2=1, 2*1.
plan factoriel

N°	A	B	AB	C	AC	BC	ABC
1	1	1	2	1	2	2	1
2	1	1	2	2	1	1	2
3	1	2	1	1	2	1	2
4	1	2	1	2	1	2	1
5	2	1	1	1	1	2	2
6	2	1	1	2	2	1	1
7	2	2	2	1	1	1	1
8	2	2	2	2	2	2	2
	A	B	AB	C	AC	BC	ABC
2	1	1	2	2	1	1	2
3	1	2	1	1	2	1	2
5	2	1	1	1	1	2	2
8	2	2	2	2	2	2	2

si on néglige les interactions d'ordre 3 on peut couper ce plan en ne prenant que les 2 de la colonne ABC on obtient.

il existe 2^3 - 1 = 7 manières de couper en deux parties (autant que de colonnes) ici A et BC sont alias c'est à dire que dans les calculs des effets de A sont confondus avec ceux de BC on calcule E(A) + E(BC)

Le demi-plan coûtera deux fois moins cher mais il est ambigu dans l'estimation de certains effets appelés alias.

Détermination des alias action A coupure ABC :
A*ABC=A^ 2BC=BC

Méthode Taguchi

4 groupes de facteurs
O difficile à modifier
@
@
* facile à modifier
O-----@ le trait représente l'interaction
tableau des interactions

1	2	3
(1)	3	2
	(2)	1
		(3)

interaction AB intersection ligne (1) colonne 2 soit colonne 3

construction d'un plan Taguchi

1. graphe linéaire du modèle
2. recherche de la table correspondante
   orthogonalité
   ddl
3. rechercher un graphe pouvant servir
   affecter les colonnes aux facteurs
   L'ordre des expériences n'a aucune influence sur les résultats mais sa modification rend caduque la classification O@@* de Taguchi
   Supposons que les 8 premiers essais A=1 soient effectués avec un lot de pièces et les 8 derniers A=2 avec un autre lot l'influence du lot serait confondue avec celle de A : il faut donc ALEARISER (tirer au hasard) les facteurs non contrôlés que l'on suppose influents leurs effets se retrouveront dans les résidus
   
4. calcul des effets et représentation graphique du modèle
5. optimisation calcul théorique études des incompatibilités (interaction qui compense les effets)
6. essai de confirmation pour vérifier l'hypothèse

Etudes des alias

une bonne préparation du terrain avec des spécialistes du système étudié évite les problèmes mais pour obtenir une certitude essayer sur un point non étudié dans le plan.
étude des interactions impossible table l12 (2^11) et l36 (2^11*3^12)

étude d'un exemple (diminuer un retrait de 1,9)
réponse théorique 0,69
essai de confirmation

cas 1 réponse 0,71 bon modèle interaction ~0
cas 2 réponse 0,45 modèle pas très satisfaisant réponse meilleure que prédite
cas 3 réponse 1,2 modèle pas très satisfaisant réponse meilleure que 1,9 : recherche des interactions
cas 4 réponse 2,5 modèle à jeter

1. mauvais choix des facteurs
2. interactions fortes oubliées
3. pas assez d'écart entre les différents niveaux des facteurs effets calculés proches variance résiduelle difficulté de calcul des effets

étude des réponses qualitatives

les études doivent porter sur des lots. Pour chaque lot on compte le nombre d'essais étant dans chaque modalité ex sur 10 lots peinture 3 modalités < bon >

A	B	<	=	>	total
1	1	2	7	1	10
1	2	5	4	2	10
2	1	2	8	0	10
2	2	0	9	1	10

table des réponses

	<	=	>
A1	7	11	2
A2	2	17	1
B1	4	15	1
B2	5	13	2

table des effets

	<	=	>
EA(A2-A1)	-5	6	-1
EB(B2-B1)	1	-2	1

Représentation graphique

Il faut donc choisir la réponse qui optimise le = ici A2, B1
estimation du résultat
Y~=Y_+E(A2)+E(B1)=28/40+(17/20-28/40)+(15/20-28/40)
EAi= moyenne niveau i - moyenne générale
Y~=70%+15%-5%=90% : mauvaise additivité des pourcentages pour y remédier on utilise la transformation oméga (log =ln10)
Og = -10 log (1/p-1)
p=1/(1+10^(-Og/10))
dans ce cas Y~=88,6% moins optimiste que 90% mais plus réaliste

Réalisation des essais par bloc

Si on ne peut réaliser tous les essais sur une même machine et que l'on ne peut aléariser les essais il faut éviter que l'effet de la machine qui peut ne pas être négligeable ne soit pas confondu avec celui d'un facteur pour cela il faut rajouter un facteur X cette colonne contiendra les effets du changement de machine et ne biaisera pas les résultats.

Les plans produits

Un produit est d'autant plus robuste que la perte pour l'entreprise est faible même dans en présence de bruits

la fonction perte L=k(Y-Y0)^2
k constante phénomène -->calculée dès que l'on connaît un point
Y0 normale cherchée
Y valeur mesurée de la caractéristique

Perte dans le cas d'un échantillons de moyenne Y_ et d'écart-type s=somme(x-x_)^2/(n-1)
L=k(s^2+(Y_-Y0)^2)
k calculé avec la formule précédente

perte dans le cas de recherche de minimum
L=k Y^2
H limite de tolérance, p perte subie par non conformité k=p/H^2

perte dans le cas de recherche de maximum
L=k*(1/Y)^2 dans ce cas k=p*H^2

à la conception d'un système il faut fixer une double optimisation.
fonctionnement optimal du système
robustesse des résultats

Plans produits et rapports signal bruit

A, B, C facteurs principaux
R,S,T facteurs bruit

un plan produit revient à étudier toutes les interactions entre les facteurs principaux et les bruits.

				1	2	3	4
			R	1	1	2	2
			S	1	2	1	2
			T	1	2	2	1
N°	A	B	C					moyennes	écart-type	S/N
1	1	1	1
2	1	2	2
3	2	1	2		Y32			ML3	s3	(voir suite)
4	2	2	1
moyennes					MC2			M

rapport signal bruit dans le cas où l'optimum est la nominale

fonction perte L=k(s^2+(Y-Y0)^2) Y0 nominale cherchée

si on modifie Y qui est la réponse actuelle pour ajuster la réponse sur Y0 il faut la multiplier dans un rapport Y0/Y. Mais dans ce cas l'écart-type va varier de la même valeur s'=s*(Y0/Y)

La fonction perte devient : L=k*s'^2 = k((Y0/Y)s)^2=k Y0^2 (s^2/Y^2)
(Y devient Y0 et s devient s')

Si nous cherchons à minimiser la perte subie, il faut minimiser s^2/Y^2 ou maximiser son inverse Y^2/s^2. Ce rapport sera utilisé sous sa forme en décibels v=10 log (Y^2/s^2) : plus ce rapport est élevé plus la perte sera faible. Le même genre de calculs donne les résultats pour les cas de recherche d'extréma.

Dans le cas d'un plan produit, il faut calculer le rapport signal/bruit pour chaque ligne du plan principal.
Dans le cas de l'étude d'un processus dans le temps il est intéressant de traiter le temps comme un facteur bruit car dans ce cas sans trop compliquer le recueil des données on a les interactions du temps avec tous les facteurs contrôlés.

Tableau d'analyse de la variance

source	somme des carrés	ddl	variances	F exp	F théo	sign?
A	SA=N * somme (EA2)/na	na-1	VA=SA/(na-1)	VA/VR	v1=na-1 v2=vr	O/N
B	SB=N * somme (EB2)/nb	nb-1	VB=SB/(nb-1)	VB/VR	v1=nb-1 v2=vr	O/N
C	SC=N * somme (EC2)/nc	nc-1	VC=SC/(nc-1)	VC/VR	v1=nc-1 v2=vr	O/N
AB	SAB=N * somme (IAB2)/(nanb)	(na-1)*(nb-1)	VAB=SAB/[(na-1)*(nb-1)]	VAB/VR	v1=(na-1)*(nb-1) v2=vr	O/N
résidus	Sr=N * somme (r2)/nc	nr=Nlignes-ddlmodèle	Vr=Sr/nr
total	ST=somme(Y-moy(Y))2	N-1

La colonne somme des carrés doit vérifier St=Sa+...+Sr
Dans le cas d'un plan avec répétition des expériences le nombre de ddl des résidus va augmenter de manière significative.

utilisation d'excel
LOI.F(x;degrés_liberté1;degrés_liberté2)
x représente la valeur à laquelle la fonction doit être évaluée.

pour calculer F théorique
INVERSE.LOI.F(probabilité;degrés_liberté1;degrés_liberté2)
probabilité représente une probabilité associée à la distribution cumulée F.
degrés_liberté1 représente le numérateur des degrés de liberté.
degrés_liberté2 représente le dénominateur des degrés de liberté.

Si un facteur n'est pas significatif on doit l'enlever du modèle et recalculer les résidus.
Si l'interaction AB est significative on gardera le facteur B même si il n'est pas significatif.

intervalle de confiance pour un coefficient du modèle
Ai=Ai calculé +- t(n-p ; alpha) * s * racine(ddl A / n)

estimation dans un noeud non observé :
y=y prévu +- t(n-p ; alpha) * s * racine(1+p/n)

estimation dans un noeud déjà mesuré
y=y prévu +- t(n-p ; alpha) * s * racine(p/n)

n expériences
p ddl modèle
t désigne la loi de student
alpha niveau de confiance
s=racine(Vr)

utilisation d'excel
t(n-p ; alpha) = LOI.STUDENT.INVERSE(1-alpha;n-p)
pour un intervalle avec un niveau de confiance alpha de 95% (+/- 2,5% d'erreur)
t(n-p, 0,95) = LOI.STUDENT.INVERSE(0,05 ; n-p)

On a intérêt à faire varier les facteurs quantitatifs les plus faciles à manoeuvrer car si on les laisse stable on risque d'introduire une dérive (exemple outil A et outil B si on fait 10 expériences avec un outil sans changer le réglage on peut biaiser les résultats à cause de l'usure de l'outil).

L'apport de Taguchi a été la création de tables standards permettant des études courantes.

Choix des modèles en général 2 stratégies possibles

1. négliger les interactions cas de recherche d'extrémum ou quand on cherche à hierarchiser les effets des facteurs.
   On ne peut retenir n'importe quelle table de Taguchi : L12 (11), L18 (2 37), L20 (219), L32 (249), L36 (313), éventuellement L8 (27) ou L16 (215)
   
2. Toutes les interactions non négligeables sont introduites dans le modèle
   but décrire finement le modèle : prédire avec précision les effets des facteurs et leurs interactions.
   

CHARGEZ ET UTILISEZ LES TABLES

Les tables suivantes font partie de la compilation qualité.

plan factoriel L8 23	table l12	table L16 (45)	table L25
table L4 (23)	plan L12 (211)	table L18	table L27 (313)
table L9	table L16	table L20	table L36
table L32 (2*49)	table L32 231

Contactez-moi pour vos questions, commentaires ou un projet.