Contrôle de réception
Les statistiques de la qualité :
- Etude de capabilité d'un procédé
- Les plans d'expériences et méthode Taguchi pour améliorer un processus
- Les cartes de contrôle pour le suivi d'un processus dans le temps.

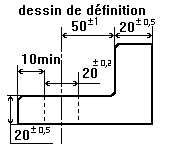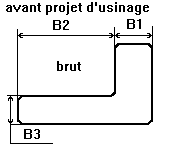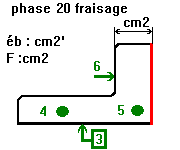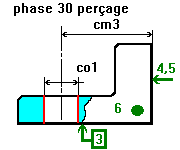
Une simulation d'usinage pour relier dessin de définition et les statistiques de la qualité.
Un nouvel ordonnancement utilisant la méthode OPT les PQR arbres et les algorithmes génétiques
Algorithme hongrois (Konig Egervary). Affectation de personnes à des tâches avec minimisation du coût total.
Un commentaire, un projet, une question : contactez moi
|
Donnez votre avis sur cette page Afin d'améliorer mon site, utilisez ce questionnaire |
Introduction
La situation :
une entreprise reçoit un lot de produit par un fournisseur : comment vérifier si la livraison est conforme aux spécifications fixées par le contrat ?
L'outil :
Utilisation d'un plan de contrôle de réception : inspection ==>information ==> décision
Il s'agit de trouver une procédure qui permet de déclarer :
lot conforme / non-conforme aux spécifications.
- lot (palette, sac, camion...) ==> N produits
- échantillon ==> n produits <N
- paramètre p : qualité du lot
Approches utilisées
- acceptation des lots sans inspection
- fournisseur sérieux - inspection 100%
- composant extrêmement critique (sécurité)
- coût très élevé - acceptation par échantillonnage
- contrôle destructif (flash)
- coût d'inspection 100% très élevé
- inspection 100% impossible
- erreurs d'inspection élevées
- le passé du fournisseur est bon
Plans de contrôle par attributs
Divers types
- type simple on tire au hasard un échantillon de pièces que l'on mesure
- n : taille d'échantillon
- a : nb maxi de mauvais (d) pour acceptation
- r : nb mini de mauvais pour rejet
avec a = r-1
- type double n1 a1 a2 il s'agit de tirer au hasard n1 pièces dans la livraison on a alors 3 possibilité, lot accepté, lot refusé, ou entre les 2 tirages de nouvelles pièces pour confirmation du choix
- lot accepté si d1<= a1
- lot refusé si d1 >= a2
- si a1<d1<a2 on tire n2 pièces
- si d1+d2<= a2 acceptation
- si d1+d2 > a2 refus
L'intérêt du plan double est qu'il est plus économique. Le gain est d'autant plus important que la probabilité d'être entre les 2 est faible (cas de production de bonnes qualité/demande).
Courbe d'efficacité d'un plan de contrôle
p est la qualité du lot : c'est la proportion de non conformes
un plan simple est défini par :
- n la taille de l'échantillon
- a le nombre d'acceptation
Si D est une variable aléatoire v.a. qui mesure le nombre de non-conformes dans un échantillon de taille n
Pa probabilité d'acceptation du lot
Pa=P{D<=a} = fonction (n, p, a) = g (n, a, p) = g (p) pour un plan (n, a) donné
Courbe d'efficacité = {(p ; Pa) / p [0..1 ]}
les chiffres de cette courbe s'obtiennent en utilisant les lois Hypergéométriques, de Bernouilli, de Poisson ou de Laplace Gauss cliquez pour obtenir leurs domaines d'application
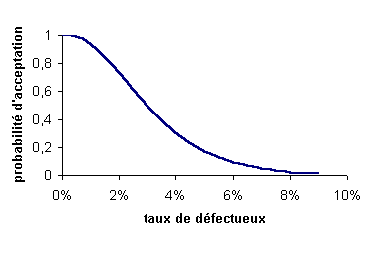
Risque du fournisseur et du client
Plusieurs lots soumis à une inspection. Même si les lots sont tous de la même qualité, le contrôle peut accepter quelques lots et en rejeter d'autres.
Les lots rejetés ne sont pas plus mauvais que les acceptés !!
- Deux types de risques
- Risque fournisseur (1ère espèce) est le risque du fournisseur de se voir refuser un bon lot.
p<= NQAcceptable - Risque client (2nde espèce) est le risque du client d'accepter un lot de qualité inacceptable.
p>= NQde Rejet
- Risque fournisseur (1ère espèce) est le risque du fournisseur de se voir refuser un bon lot.
Choix d'un plan
Le plan de contrôle, (la courbe d'efficacité), est déterminée par deux points.
Le premier point associe à une valeur faible p=NQA, caractérisant une qualité acceptable une probabilité petite alpha que le lot soit rejeté, donc une probabilité grande 1-alpha qu'il soit accepté.
tout lot de qualité p<= NQA a une probabilité au plus égale à alpha d'être rejeté donc au moins égale à 1-alpha d'être accepté.
Le second point associe à une valeur p=NQR correspondant à une qualité considérée comme inacceptable une probabilité, également petite bêta que le lot soit accepté. Bêta est le risque du client (accepter un lot de qualité p>= NQR)
Tout lot de qualité p>=NQR a une probabilité au plus égale à bêta d'être accepté, donc une probabilité au moins égale à 1-bêta d'être rejeté.
La courbe d'efficacité doit passer par
A (NQA ; 1-alpha)
B (NQR ; bêta)
ceci donne n, a, r=a+1.
Les équation déterminant n et a sont différentes suivant les lois utilisées cliquez pour obtenir leurs domaines d'application
Utilisation d'un graphique
Dans le cas général on utilise un graphique appelé nomographe, ici pour la loi binomiale.
Sur l'échelle de gauche on note NQA et NQR.
Sur l'échelle de droite on note bêta et 1-alpha
on relie NQA à 1-alpha et NQR à bêta.
l'intersection se fait sur le quadrillage et on note n et a
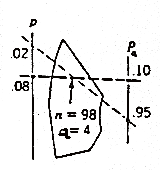
Voir le graphique taille réelle
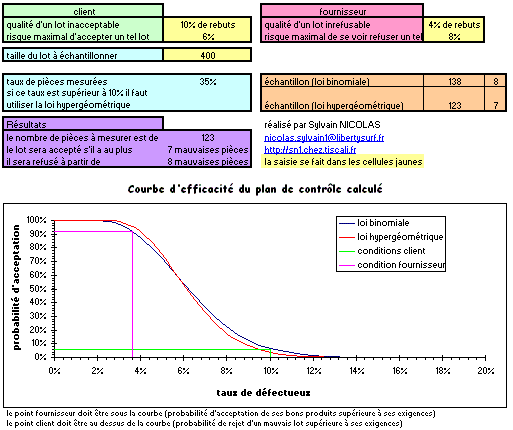
Utilisation d'excel
Pour les personnes disposant d'excel j'ai fait un classeur qui calcule le plan automatiquement : on saisit les 4 paramètres plus la taille du lot à échantillonner (cellules jaunes). Le plan est alors calculé en tenant compte du taux de pièces contrôlées (loi binomiale ou hypergéométrique). La courbe d'efficacité est présentée en même temps.
Que faire d'un lot refusé ?
Les programmes de contrôle de réception demandent en général des actions correctives quand les lots sont refusés.
lot refusé :
faire retourner chez le fournisseur
contrôle à 100% avec remplacement des pièces défectueuses.
Ces actions sont appelées rectification des programmes d'inspection, qui sert à rendre correcte la qualité des lots.
au départ lot de qualité P0,
après le contrôle lot de qualité P*
P* <= P0
Qualité moyenne après le contrôle
QMT = qualité moyenne transmise
AOQ = average outgoing quality
Calcul de QMT
N taille du lot
p la qualité du lot avant le contrôle
n, a le plan
P* = ?
K v.a. nombre de pièces non conformes dans le lot après le contrôle
|
K
|
0
|
(N-n)p
|
|
proba
|
1-Pa
|
Pa
|
E(K)=p*Pa*(N-n)
QMT=E(K)/N=p*Pa*(N-n)/N
Les équation déterminant Pa = probabilité d'acceptation sont différentes suivant les lois utilisées cliquez pour obtenir leurs domaines d'application
Exemple de gestion client fournisseur à l'aide de ces outils :
Le contrôle statistique vient du fait que l'on ne peut pas tout mesurer (pb temps ou contrôle destructif). Il faut donc trouver un compromis. Les pourcentages sont le résultat d'une négociation sauf s'il existe une norme dans votre domaine d'activité.
Il faut voir que même s'il n'y a que quelques mauvaises pièces, elles seront peut-être dans l'échatillon mesuré et le lot sera refusé c'est le risque du fournisseur. D'autre part il peut y avoir un lot avec plein de mauvaises pièces et l'échantillon mesuré être ok, c'est le risque du client.
Le client peut dire moi je veux pas qu'il y ait plus de 10% de rebut et si ça arrive il faut pas que ça passe, à la rigueur une fois tous les 5 ans.
On peut alors compter en se disant, on a une livraison par semaine sur 5 ans ça fait 250 livraisons. Par expérience on sait qu'il y a 20% de livraisons avec plus de 10% de rebuts. Ca fait 50 mauvaises livraisons, si on accepte d'en faire passer une ça fait un risque de 2%.
Le fournisseur peut raisonner autrement et se dire, moi, ce que je veux pas c'est qu'il me renvoie un camion où il n'y a que 5% de mauvaises pièces. On a un accord qui veut que si le camion est renvoyé, il faut rechercher les rebuts et les remplacer par des bonnes pièces pour que taux de rebuts tombe en dessous de 7% et dans le cas présent ça équivaut presque à tout recompter (puisque le premier comptage laisse à penser qu'il y a au moins 10% de mauvaises pièces). A la rigueur on peut faire ça une fois par an mais pas plus (on fait déjà un recomptage une fois par mois pour de vraies mauvaises livraisons).
On a mesuré que 60% de nos livraisons avaient moins de 5% de mauvaises pièces. Cela fait 30 livraisons par an, si on en accepte une cela fait 3.33%.
Là le calcul montre que le nombre de pièces à mesurer sera de 417, comme les lots livrés sont de 1000 ça fait trop à mesurer. Et donc là, il faut que chacun lache un peu. Si les 2 cèdent sur le taux inacceptable les mesures seront pour 11% client et 4% coté fournisseur, cela fait un plan de mesure de 198 mesures soit la moitié.
Après il faut savoir évaluer combien coûte la mesure et anticiper sur la qualité des futures livraisons. En cela, le classeur Excel permet de faire des simulations plus facilement que le graphique.
Autre manière de contrôler :
Ce plan de contrôle est indiqué aux attributs car il présente la pièce comme étant bonne ou mauvaise. Souvent, cette manière de vérifier se base sur une seule valeur dépassant ou pas des limites mini ou maxi. Or dans la réalité, on a plusieurs variables et si on se concentre sur chacune d'elle on ne voit pas les variations, certes plus petites mais qui étant simultanées peuvent indiquer un changement profond.
- Cela peut être utile au fournisseur en complément de cartes de contrôles individuelles
- Cela peut être utilie au client
- pour détecter des modifications de processus de production chez le fournisseur.
- pour détecter des fraudes