Recherche opérationnelle
- les plans d'expériences et méthode Taguchi
- les cartes de contrôle pour le suivi d'un processus dans le temps.

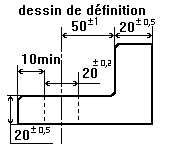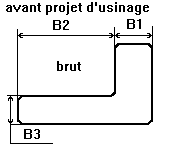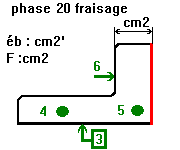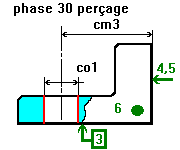
une simulation d'usinage pour relier dessin de définition et les statistiques de la qualité.
Un nouvel ordonnancement utilisant la méthode OPT les PQR arbres et les algorithmes génétiquesAlgorithme hongrois (Konig Egervary). Affectation de personnes à des tâches avec minimisation du coût total.
présentez moi
votre projet
les files d'attenteLes cas de présence des files d'attente dans la vie quotidienne sont nombreux :
Mais cela peut être aussi :
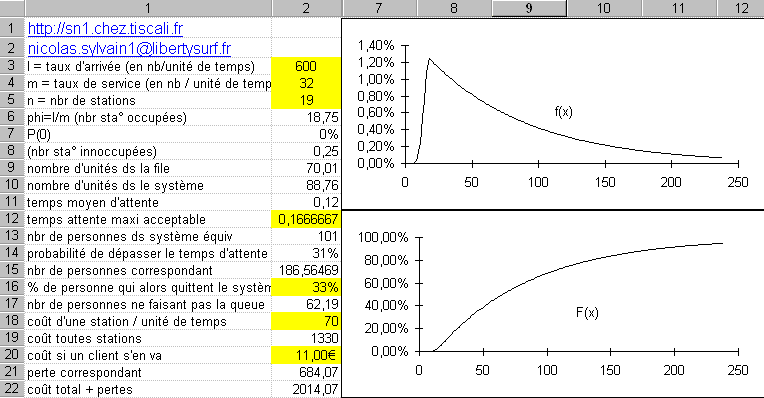
Le cas présenté ici est le cas classique où le taux d'arrivée est constant et ou le nombre d'entrées ou de sorties par unité de temps suit une loi de poisson. La première chose à fair lorsque l'on va faire une étude de files d'attentes c'est de définir une unité de temps : seconde, minute, heure, jour... Une autre chose importante c'est de considérer des périodes de temps où le nombre d'unités se présentant dans le système reste le plus stable possible. Mettons nous dans le cas d'un magasin où il rentre 10 clients par minute sur une période de 4 heures tous les jours : combien de caissières doit il faire travailler pendant cette période. Prenons comme référence l'heure, il rentre donc 600 clients / heure, on reporte ce nombre L3C2. Il faut maintenant estimer combien une caissière est capable de servir de clients en une heure. Pour ce faire il faut prendre garde à dire : hier elle a travaillé 4 heures et servi 120 clients donc elle sert 30 clients à l'heure. En effet, si elle a effectivement servi 120 clients en 4 heures il ne s'est pas présenté de clients pendant 3 périodes de 5 minutes, son taux de service est donc 120/3,75=32 . Une autre manière de parvenir à ce chiffre est de calculer le temps moyen de service d'un client puis de diviser 1 heure par ce temps en heures. Ce nombre va être mis en L4C2. Vous savez maintenant que vous devez ouvrir au moins : 600/32 = 18.75 soit 19 caisses pour éviter l'engorgement.
Que sait-on dans ce cas là : le nombre de caisses où il n'y a personne est de 0.25/19 ce qui correspond à peu près à 50 secondes par caisse et par heure. Le nombre de personnes dans la file d'attente est de 70 L9C2 (3,68/caisse) auquel il faut rajouter la personne en train de se faire servir pour avoir le nombre total d'unités dans le système L10C2. et le nombre de personnes dans la file va donner le temps moyen d'attente L11C2 ici 7 minutes. Maintenant voyons une application de ce tableau : Supposons que si le temps d'attent est trop grand 10 minutes par exemple (soit 10/60=0.166 heures L12C2) alors une proportion de clients 1/3=33,33% L15C2 déposent leurs achats et quittent le magasin celui-ci perd sa marge de 11€ L20C2 On peut ainsi faire des simulations pour regarder en fonction du coût d'une station supplémentaire si les clients récupérés compensent cette dépense. Pour faire des simulations vous avez deux outils dans excel : les tables (menu données) et le gestionnaire de scénarios (menu outils). Le document Excel contenant l'onglet faisant ces calculs est le classeur faisant aussi l'algorithme hongrois. |