Analyse de Capabilité
- plan de contrôle de réception.
- étude de capabilité d'un procédé
- les plans d'expériences et méthode Taguchi
- les cartes de contrôle pour le suivi d'un processus dans le temps.

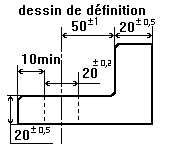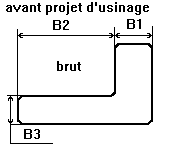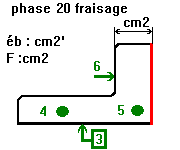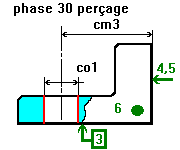
une simulation d'usinage pour relier dessin de définition et les statistiques de la qualité.
Un nouvel ordonnancement utilisant la méthode OPT les PQR arbres et les algorithmes génétiquesAlgorithme hongrois (Konig Egervary). Affectation de personnes à des tâches avec minimisation du coût total.
Sommaire
- Introduction
- Outils
- Indices de Capabilité
- Estimation de l'indice Cp
- Indice Cpk
- La capabilité machine Cm et Cmk
- Capabilité pour une variable non normale
- Conclusion
- Classeur excel à Télécharger
Introduction
La capabilité est une analyse importante car la qualité est la satisfaction du client. Or le calcul de capabilité fait entrer dans le calcul statistique les besoins du client. C'est le moment où l'entreprise peut vérifier qu'elle est en mesure de répondre à un cahier des charges. Les calculs présentés ci dessous se font donc avec des pièces déjà produites. Des calculs de capabilité toutes les étapes du processus permettent de pouvoir estimer la capabilité dès la conception par simulation.
procédé = combinaison de 5M (Main-d'œuvre, Matériaux, Machines, Méthodes, Mesures)
X = caractéristique de qualité
Capabilité : aptitude d'un procédé de production ou d'un moyen à respecter des spécifications.
AFNOR X06-030
Un processus sera déclaré "apte" s'il a démontré, pour les caractéristiques sélectionnées, qu'il étatit capable de produire pendant une période suffisemment longue, avec un taux théorique de non-conformités inférieur aux exigences internes à l'entreprise ou contractuelles.
Ce taux est fréquemment fixé à 0,27% (méthode six sigma)
Outils :
- histogramme,
n=50-100 ou plus,
avantage vision immédiate de la performance du procédé
- droite de Henry
avantages :
- pas de division en classes
- résultats raisonables pour n petit 15-20-30-40
- indices de Capabilité Cp Cpk Cm Cmk
Indices de Capabilité
Calculs dans le cas d'une variable normale X (m, s),
Ti limite de spécification inférieure,
Ts limite de spécification supérieure
Les valeurs de X en dehors des limites sont appelées "non-conformes"
le taux de non-conformes est minimum si m=(Ti+Ts)/2 (processus centré)
Indice Cp mesure d'aptitude potentielle
Cp=(Ts-Ti)/(6s) >> 2 spécifications
Cp=(Ts-m)/(3s) >> une seule spécification Ts
Cp=(m-Ti)/(3s) >> une seule spécification Ti
Remarque
Cp = 1 ne garantit pas qu'il peut avoir seulement 0,27% de non conformes.
La proportion espérée de NC ne sera jamais moins de 0,27% (X suit une loi normale)
les grandes valeurs de Cp ne garantissent pas l'acceptabilité en l'abscence de l'information sur la valeur centrée du procédé
Valeurs minimum recommendées pour Cp (Montgomery 1985)
| 2_spécifications | une spécification | |
| processus existant | 1,33 | 1,25 |
| nouveau processus | 1,50 | 1,45 |
| paramètre de sécurité ou critique processus existant | 1,50 | 1,45 |
| paramètre de sécurité ou critique, nouveau processus | 1,67 | 1,60 |
Autres pays Sullivian 1985
multidimensionnelles Kots and Johnson 1993
Actuellement, les grands constructeurs automobiles ( PSA, RSA, FORD) imposent :
Cp=1.67, CPK=1.33
Estimation de l'indice Cp
x1,..., xn avec n = 50-100 ou plus
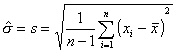
utilisation d'excel
s = ECARTYPE(nombre1;nombre2;...)
si X suit une loi normale alors :
![]()
intervalle de confiance de niveau 1-alpha pour sigma :
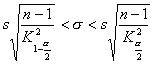
utilisation d'excel
K2(p)=KHIDEUX.INVERSE( p ; n-1 degrés_liberté)=k/p(x>k)=p
intervalle de confiance de niveau 1-alpha pour Cp :
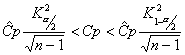
Indice Cpk
Cp n'exige pas la connaissance de la moyenne pour son évaluation. L'indice Cpk est introduit afin de donner une certaine influence à la moyenne.
Cpk=min{CPL, CPU}
CPL= (m-Ti)/3sigma
CPU=(TS-m)/3sigma
- Cp et Cpk supérieurs à 1 procédé capable et bien centré
- Cp>1 et Cpk<1 procédé capable et mal centré
- Cp<1 procédé non capable
La capabilité machine Cm et Cmk
les calculs de Cm et Cmk se font à partir de 50 pièces fabriquées de manière consécutive sans changer de réglage. Lorsqu'une pièce passe à travers différentes machines les variances s'ajoutent c'est pourquoi on est plus exigent pour Cm que pour Cp. Cm doit être supérieure à 1,33 (4 écarts-types).
- Cm et Cmk supérieurs à 1,33 machine capable et bien centrée
- Cm>1,33 et Cmk<1,33 machine capable et mal centrée
- Cm<1,33 machine non capable
Capabilité pour une variable non normale
Remarque :
Si la loi est non normale, avant de faire les calculs de Cp et Cpk, nous devons nous interroger sur la non présence de causes assignables (changement de lot...).
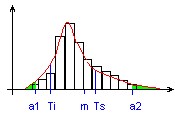 a1=>0,135%, a2=99,865%
a1=>0,135%, a2=99,865%
![]()
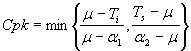
pour Cpk utiliser la médiane si la loi est fortement asymétrique
Conclusion
Après une étude de capabilité on se trouve devant deux possibilités
- le processus ou la machine est capable, il faut encore le vérifier dans le temps on utilisera donc les cartes de contrôle avec un journal de bord.
- le processus ou la machine n'est pas capable il faut donc trouver les causes de ces variances ou décalages et pour cela on peut utiliser les plans d'expériences pour faire des tests de manière économique et facilement interprétable.
La connaissance des capabilités et donc des variances de chacune des machines de l'atelier permet de prévoir notre capabilité à produire une nouvelle pièce sans faire de nouveaux essais à l'aide d'une simulation d'usinage.
Classeur Excel à télécharger
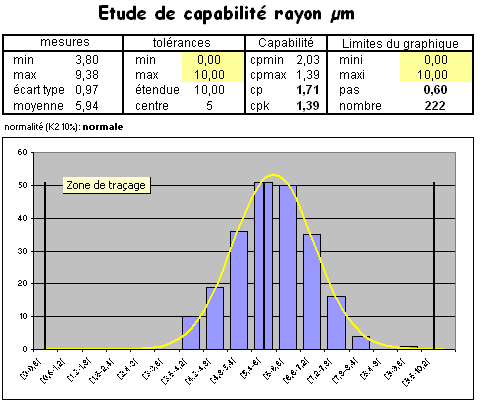
Pour les calculs de capabilité simples j'ai conçu ce tableau. il est composé de deux onglets
- un onglet de saisie dans lequel vous utiliser une colonne pour inscrire vos mesures,
- l'onglet de visualisation présenté ci dessous :
- on y fait la saisie des informations complémentaires dans les cellules jaunes
- le reste du tableau se remplit automatiquement avec les calculs faits à partir des mesures. Une indication est faite sur la normalité de la distribution.
- un graphique reprend les données avec 3 courbes
- les données sous forme de barres,
- une courbe en cloche ayant les paramètres de moyenne et ecart type des mesures
- des barres verticales signifiant les moyennes de la mesure ainsi que les limites de tolérances.
Analyse de la capabilité des instruments de mesures (cg, cgk)
Les cartes de contrôle
Les plans d'expériences
Mes coordonnées