Recherche opérationnelle
Les statistiques de la qualité :
- plan de contrôle de réception.
- étude de capabilité d'un procédé
- les plans d'expériences et méthode Taguchi
- les cartes de contrôle pour le suivi d'un processus dans le temps.

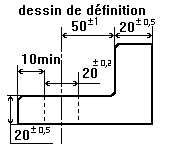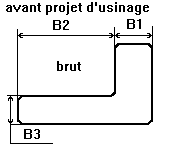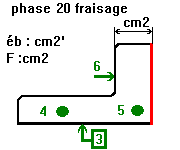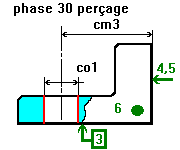
Une simulation d'usinage pour relier dessin de définition et les statistiques de la qualité.
Un nouvel ordonnancement utilisant la méthode OPT les PQR arbres et les algorithmes génétiquesAlgorithme hongrois (Konig Egervary). Affectation de personnes à des tâches avec minimisation du coût total.
présentez moi
votre projet
algo hongroisCet algorithme est prévu pour minimiser une somme. Exemple de problème affectation de coût minimal
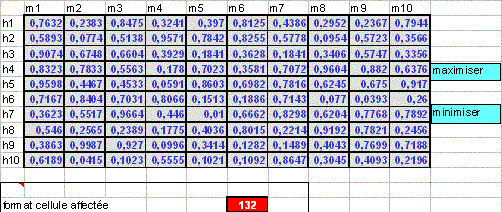
Un conseil municipal a décidé de favoriser trois entrepreneurs A, B et C susceptibles de fournir des produits x, y et z, à des prix donnés par le tableau suivant : détail de l'algorithme : 1 on soustrait ligne par ligne et colonne par colonne le plus petit élément. 2 si on peut affecter un zéro par ligne et par colonne on a la solution optimale 3 sinon on choisit au hasard une affectation de 0. Ces 0 choisis sont dits 0 encadrés ; les autres sont dits 0 barrés 4 marquer toute ligne n'ayant pas de 0 encadré. 5 marquer toute colonne ayant un 0 barré dans une ligne marquée 6 marquer toute ligne ayant un 0 encadré dans une colonne marquée 7 revenir à 4 jusqu'à marquage impossible 8 tracer un trait sur les lignes non marquées et les colonnes marquées 9 prendre le plus petit chiffre du tableau restant et le retrancher de tous les éléments non rayés et l'ajouter aux éléments rayés deux fois. 10 reprendre à 2 Utilisation d'excel J'ai créé un classeur Excel utilisant cet algorithme d'affectation pour une matrice de 10*10. C'est un document semi automatique : il fait le marquage et les calculs et vous faites l'étape 2 simplement à la souris. La première chose à faire est de remplir la matrice des coûts. Les valeurs saisies il faut choisir un format pour les cellules qui seront solution (c'est ici la cellule rouge). Tout est prêt alors on se lance en choisissant le bouton minimiser ou maximiser.
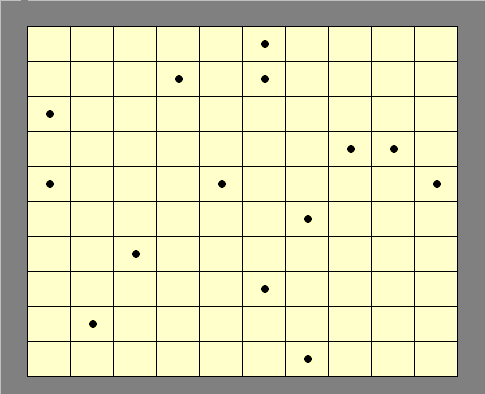
Ce lancement copie les valeurs dans l'onglet intermédiaire et alors on se trouve devant un écran comme celui-ci.
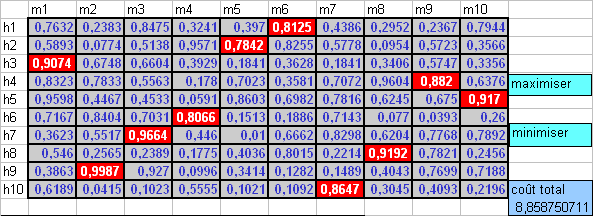
Les points représentent les 0 à choisir. Il ne doit y en avoir qu'un seul par ligne et par colonne. Pour effacer les surnuméraires, il suffit de cliquer dans la cellule. Le choix est souvent simple. Par exemple dans la colonne 1 il y a deux possibilités, mais on voit que dans la cinquième ligne, il y a plusieurs points donc on va effacer le premier. Après quelques boucles on trouve une solution (on remarque le coût indiqué en bas à droite) :
Contactez-moi pour tout projet du plus modeste au plus évolué. |